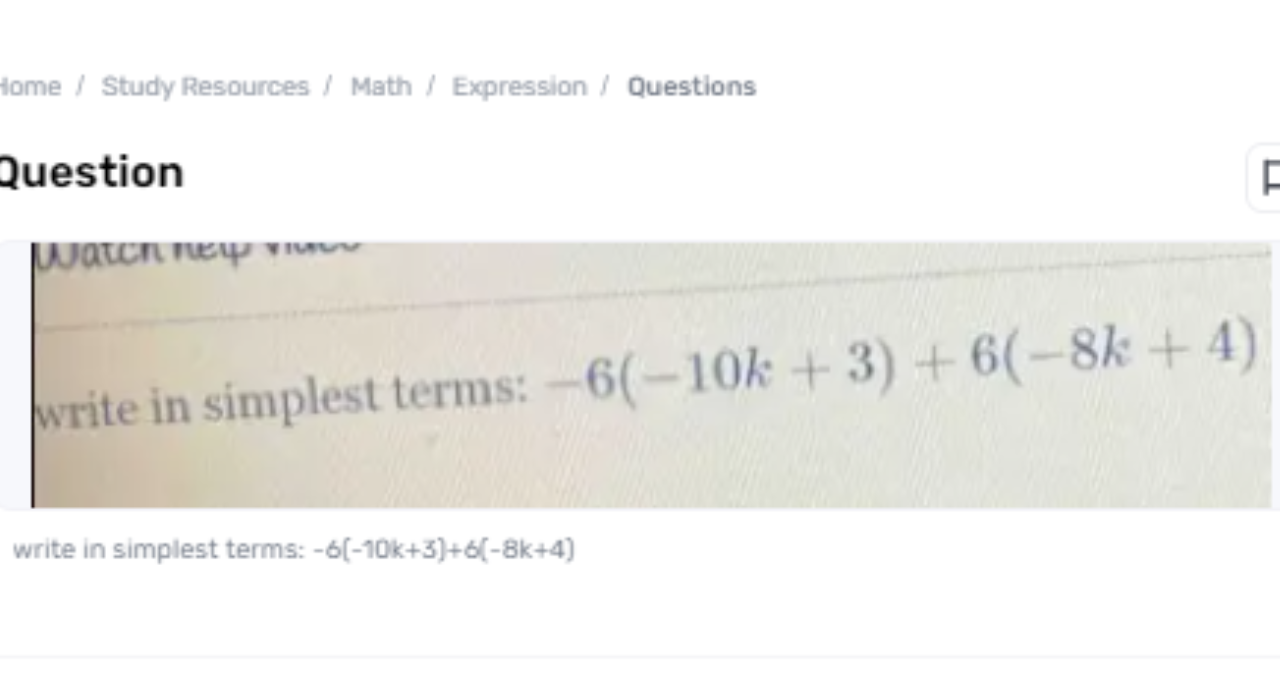
In geometry, understanding the properties of shapes such as squares is fundamental for tackling different numerical issues. One essential property of a square is its edge, which is the entire remove around the shape. Given the border of a square, one can decide the length of each side, which is pivotal for tackling issues related to ranges, volumes, and other geometric calculations. In this paper, we'll investigate the issue the perimeter of square jklm is 48 units. what is the value of x? 6 9 12 15 of finding the esteem of x when the edge of square JKL, is 48 units, and decide which of the given options 6, 9, 12, or 15 is adjusted.
Understanding the Border of a Square
The border of a square is calculated by including the lengths of all four sides. Since all sides of a square rise, the border P can be communicated as P=4s, where sss is the length of one side. This relationship emerges from the truth that a square has four break-even sides, and the border is the whole of these sides. For example, if each side of a square is 10 units long, the edge would be 4*10=40 units.
Applying the Perimeter Formula
Given that the border of square JKL is 48 units, we are ready to utilize the border equation to find the length of one side. Utilizing the equation P=4s, where P is the edge and sss is the side length, ready to set up the condition as follows: 48=4s. To illuminate for sss, we separate both sides of the condition by 4: s=48/4=12 Hence, each side of the square is 12 units long. This calculation gives us the side length of the square, which is fundamental for confirming the alternatives given.
Assessing the Alternatives
The issue presents four conceivable values for x: 6, 9, 12, and 15. To decide which esteem is adjusted, we compare our calculated side length with these choices. Since we have decided that each side of the square is 12 units long, the right esteem for x is straightforwardly found from the alternatives given.
1. Option 6: On the off chance that each side was 6 units, the edge would be 4 * 6=24, which does not coordinate the given edge of 48 units.
2. Option 9: On the off chance that each side was 9 units, the edge would be 4 * 9=36 units, which does not rise to 48 units.
3. Option 12: On the off chance that each side was 12 units, the border would be 4 * 12=48 units, which matches the given edge.
4. Option 15: If each side was 15 units, the edge would be 4 * 15=60 units, which surpasses the given perimeter.
Approach for Overseeing a Gauth Request
Clarify the Request:
Start by distinguishing whether the address relates to the setup, usefulness, organization, or investigation of Gauth. Understanding the particular range of concern makes a difference in creating a centered and pertinent reaction. For case, on the off chance that the request is almost establishment issues, your reaction ought to address common setup issues and arrangements.
Accumulate Important Subtle elements:
Following, collect the essential data by counseling Gauth’s official documentation and back materials. It is significant to audit client guides, FAQs, and common issues detailed by other clients. This guarantees that your reaction is based on exact and comprehensive data, tending to potential issues and giving dependable arrangements.
Build the Answer:
Organize your reaction clearly and coherently. Display the data step-by-step, giving noteworthy enlightening or arrangements that straightforwardly address the particular perspectives of the address. This organized approach makes a difference in making the reaction simple to take after and execute.
Confirm and Alter:
At last, survey the precision of the subtle elements given and refine your reaction for clarity and brevity. Guarantee that your reply is exact and free from pointless data, making it clear and simple to get it. This step guarantees that your reaction is both valuable and available to the inquirer.
Conclusion
In conclusion, the right esteem of x is 12 units. This esteem is reliable with the calculation of the side length determined from the given border of 48 units. The other options 6, 9, and 15 do not match the specified edge when connected to the equation for calculating the border of a square. Understanding the relationship between the side length and edge of a square is pivotal for understanding such geometric issues. By applying the border equation, we affirmed that the side length of square JKL, is without a doubt 12 units, making x=12 the exact choice among the given choices.